1105. Привет, Пирог!

Пиццерия Pizazz гордится тем, что она доставляет пиццу своим покупателям как можно быстрее. К несчастью, для доставки может быть нанят только один водитель. Перед развозкой он ждет, пока не поступит определенное количество заказов (от 1 до 10). Водитель предпочитает выбрать для развозки всех заказов самый быстрый путь, даже если придется проезжать несколько раз одно и то же место, включая пиццерию. В конце развозки водитель обязан вернуться в исходное место, то есть в пиццерию. Вам необходимо написать программу, которая выберет такой маршрут.

Вход. В первой строке находится количество заказов n (1 ≤ n ≤ 10). Далее следует n + 1 строка, каждая из которых содержит n + 1 целое число. Эти числа указывают на время проезда между пиццерией (ее номер 0) и n местами, где находятся заказы (они пронумерованы числами от 1 до n). j-ое значение i-ой строки указывает на время, за которое можно проехать напрямую из места i в место j, не посещая по пути никаких других мест. Заметим, что проезд между i и j может быть быстрее не напрямую, а через другие места из-за пробок на дорогах и присутствия светофоров. Время проезда не симметрично. То есть время, за которое можно напрямую проехать из i в j, не всегда совпадает с временем проезда напрямую из j в i.

Выход. Выведите одно число – наименьшее время, за которое можно развести пиццу всем заказчикам и вернуться обратно в пиццерию.

Пример входа	Пример выхода
3 0 1 10 10 1 0 1 2 10 1 0 10 10 2 10 0	8

РЕШЕНИЕ

графы – Гамильтонов цикл

Анализ алгоритма

При помощи алгоритма Флойда – Уоршела строим матрицу m, в которой m[i][j] содержит наименьшее время, за которое можно доехать из i в j.

Далее можно используя матрицу m полным перебором (используя бектрекинг) найти Гамильтонов цикл наименьшего веса. Это решение даст Time Limit.

Для прохождения по времени следует реализовать динамику на масках как в задаче комивояжера.

Пример

Слева изображен входной граф. Справа – граф кратчайших расстояний.

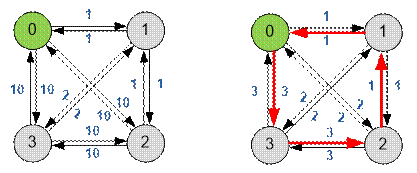
Оптимальный путь будет 0 → 1 → 3 → 1 → 2 → 1 → 0 длины 8.

Реализация алгоритма

Определим переменную INF, условно равную бесконечности, максимально возможное число вершин в графе MAX и массив dp, в котором будем хранить динамически пересчитываемые значения dp(S, i). Каждое подмножество S будем хранить в виде числа, в котором i - ый бит равен 1, если вершина с номером i в нем присутствует, и нулю иначе. Например, при n = 5 подмножество {1, 4, 5} кодируется числом 11001₂ = 25.

#define MAX 22

#define INF 0x3F3F3F3F

int dp[1<<MAX][MAX+1];

Время проезда между пунктами храним в массиве m.

int m[MAX][MAX];

Функция solve вычисляет значение dp(S, last), где множество S кодируется целым числом mask. При этом S \ {last} равно mask ^ (1<< last). Далее перебираем все i, i ΠS \ {last} и ищем минимальное значение res среди dp(S \ {last}, i) + m[i][last]. Переменная res указывает на ячейку dp[mask][last], так что с изменением res изменяется и само значение dp[mask][last].

int solve(int mask, int last)

{

int &res = dp[mask][last];

if(res == INF)

{

mask ^= (1 << last);

for(int i = 1; i < n + 1; ++i)

if(mask & (1 << i)) res = min(res,solve(mask,i) + m[i][last]);

}

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%d",&n);

for(i = 0; i < n + 1; i++)

for(j = 0; j < n + 1; j++)

scanf("%d",&m[i][j]);

При помощи алгоритма Флойда – Уоршела вычисляем кратчайшее время проезда между всеми парами мест.

for(k = 0; k < n + 1; k++)

for(i = 0; i < n + 1; i++)

for(j = 0; j < n + 1; j++)

if (m[i][k] + m[k][j] < m[i][j]) m[i][j] = m[i][k] + m[k][j];

Изначально значения dp(S, i) неизвестны, положим их равными плюс бесконечности. Множеству {0} соответствует маска 1, положим dp({0}, 0) = 0 (минимальный путь из нулевой вершины в нее же без посещения других вершин равен нулю). В переменной best храним искомую минимальную длину пути.

memset(dp,0x3F,sizeof(dp));

dp[1][0] = 0; best = INF;

Положим dp({0, i}, i) = m[0][i] (вершина 0 – местоположение пиццерии).

for(i = 1; i < n + 1; i++) dp[1 | (1 << i)][i] = m[0][i];

Вычисляем гамильтонов цикл минимальной длины. Значение 2ⁿ⁺¹ – 1 соответствует множеству {0, 1, 2, ..., n}. Вычисляем минимум среди всех значений dp({0, 1, 2, ..., n}, i) + m[i][0], 1 £ i £ n.

for(i = 1; i < n + 1; i++)

best = min(best, solve((1 << (n + 1)) - 1,i) + m[i][0]);

Выводим искомую минимальную длину пути.

printf("%d\n",best);